Dos enfoques objetivos para responder a cómo se obtiene la probabilidad de un suceso que presuponen que la probabilidad de un suceso es un dato objetivo que la persona conoce o no:
Probabilidad de un suceso aleatorio (S): cociente entre el número de resultados favorables del suceso aleatorio y el número total de resultados posibles
Probabilidad de un suceso: frecuencia relativa del mismo después de haberlo repetido un número razonablemente grande de veces
Procedimientos que sirven para juegos de azar pero no tanto en la vida diaria; por eso se utilizan las probabilidades subjetivas: derivadas de la información a disposición o las creencias u opiniones del individuo.
Según la teoría de la probabilidad, la probabilidad debe seguir los siguientes axiomas:
la probabilidad de un suceso es igual o mayor que 0. No existen probabilidades negativas.
la probabilidad de un suceso seguro es 1. La probabilidad de no ocurrencia es: P(no S)= 1 – P(S)
si dos sucesos (S1y S2) son mutuamente excluyentes entre sí, la probabilidad de uno u otro será igual a la suma de sus probabilidades:
P(S1ó S2) = P(S1)+ P(S2)
si la probabilidad de un suceso P(S2) no es igual a 0, entonces P(S1 y S2) = P(S1 asumiendo que S2) x P(S2). La probabilidad de la conjunción de dos sucesos es siempre menor o igual que la probabilidad de uno de los sucesos considerado aisladamente.
Thomas Bayes añadió una fórmula conocida como teorema de Bayes mediante el cual se puede hallar la probabilidad de un suceso a la vista de una información nueva. Esta probabilidad condicional se obtiene:
- de la probabilidad inicial, a priori, del suceso
- de la diagnosticidad del dato con respecto al suceso, es decir, en qué medida se asocian ambos, P(D/H) y P(D/H ́)
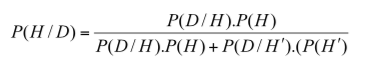
La teoría bayesiana permite introducir probabilidades subjetivas al evaluar las probabilidades a priori y las probabilidades condicionales del suceso. Por tanto, parece adecuado para situaciones de incertidumbre donde hay que realizar un juicio.
P(H): probabilidad a priori de la hipótesis: probabilidad a priori de conseguir el puesto de trabajo sin tener experiencia práctica (0.05). Probabilidad objetiva a favor.
P(H’): probabilidad de la hipótesis alternativa: probabilidad a priori de no conseguir el puesto de trabajo sin tener experiencia previa (0.95). Probabilidad objetiva en contra.
P(H/D):probabilidad de la hipótesis supuesto un dato: probabilidad de obtener plaza, habiendo sacado un 8,6 en el examen. Probabilidad estimada o a posteriori.
P(D/H): probabilidad del dato cuando se cumple la hipótesis: probabilidad de obtener buena nota en el examen y conseguir el trabajo (0.98). Probabilidad a favor condicionada al dato.
P(D/H’): probabilidad del dato cuando se cumple la hipótesis alternativa: probabilidad de obtener buena nota en el examen y no conseguir el trabajo (0.10). Probabilidad condicionada al dato pero en contra de la hipótesis.

Aumenta la probabilidad un puesto de trabajo en la empresa de un 0,05 a un 0,34.
Enfoque de los heurísticos de razonamiento
Los primeros intentos de comparar a conducta ideal, especificada por el teorema de Bayes, y el rendimiento de las personas, mostraron que las personas no utilizaban el teorema al emitir juicios de probabilidad, puesto que se apreciaba una tendencia conservadora: se integraba la información sobre el nuevo dato para producir unas probabilidades a posteriori, más cercanas a las probabilidades a priori, que las predichas por el teorema de Bayes.
En investigaciones posteriores se observó que se ignoraban las probabilidades a priori, produciéndose juicios más extremos.
Tversky y Kahneman: los juicios, no solo no seguían la norma estadística, sino que se producían errores sistemáticos.
La Teoría de la Racionalidad Restringida (Simon): debido a las limitaciones cognitivas, las personas construyen modelos simplificados del mundo, en los que posteriormente basan sus juicios y decisiones, no buscando un beneficio máximo sino un resultado satisfactorio con menor coste cognitivo.
Se trataría de centrarse en cómo se lleva a cabo la tarea realmente más que en cómo debería realizarse.
Tversky y Kahneman: las personas no muestran un razonamiento estadístico, sino que utilizan heurísticos que se aplican espontáneamente, en una gran variedad de tareas, y que son muy difíciles de eliminar, aun cuando conducen a juicios erróneos.
Esta especie de reglas permiten simplificar la tarea de asignar probabilidades y la tarea de predecir, y su uso se explica por las restricciones cognitivas, ya que raramente se puede tener en cuenta toda la información, por lo que se selecciona dependiendo del tipo de juicio a realizar y de su disponibilidad.
Heurístico de representatividad
Consiste en asignarle probabilidad a un suceso en función de su pertenencia a una clase. Es decir, se trata de juzgar la probabilidad de que A pertenezca a un conjunto B, fijándose en la semejanza entre A y los miembros de B.
El juicio se basa en determinar si el suceso u objeto en cuestión es representativo de una clase: juicio de representatividad. Si se decide que lo es, se juzgará que es probable que pertenezca a esa clase: juicio por representatividad.
El juicio de representatividad se realiza comparando las semejanzas que tiene el caso con el prototipo de su categoría. Una vez realizado este juicio, la asignación de probabilidades se realiza por la representatividad del suceso.
Sesgos y su mecanismo de acción son:
1) Insensibilidad al tamaño de la muestra:
La probabilidad asignada será más cercana a la probabilidad real del suceso cuanto mayor sea el número de observaciones de que partimos. Sin embargo, el tamaño de la muestra no parece ser importante para la mayoría de las personas.
El hecho de esperar que la frecuencia real de un suceso se manifieste en muy pocos ensayos, es un error muy frecuente, y origina la falacia del jugador: suponer que la ruleta ha de pararse en el rojo tras una serie de aradas en el negro.
Las personas tienden a extraer concusiones sobre la frecuencia de un suceso, de un acontecimiento o de una característica, a partir de muy pocas observaciones, generalizando a partir de muestras pequeñas si éstas son representativas.
Explorador en una isla desconocida. Pero, ésta generalización, no se da siempre en la misma medida, sino que las personas tienen en cuenta la homogeneidad que presenta el grupo con respecto a la característica en cuestión.
Las personas no generalizan y tienen en cuenta el tamaño de la muestra cuando se les pregunta por ciertas características (color o anidación de los “sheerables”, y sobre todo sobre la obesidad de los “barratos”) mientras que sí generalizan a partir de una sola observación en el caso de otras características (propiedades del “floridium” o el color de los “barratos”).
Esta diferencia se debe a la homogeneidad o heterogeneidad de las características:
• Los sujetos esperan que las propiedades de un mineral (“floridium”) sean estables, y generalizan a partir de una sola observación.
• Pero, la obesidad o la delgadez, se consideran características variables, por lo que solo generalizaran ante un número elevado de observaciones
2) Insensibilidad a las probabilidades a priori
Tendencia de los sujetos a asignar probabilidad a un suceso teniendo sólo en cuenta la información nueva proporcionada, cuando esta se considera representativa. Es decir, se desconoce la frecuencia real del suceso dejándose llevar por una información representativa.
Problema de Tom 3 grupos:
1. Debía evaluar la frecuencia en la población de un listado de profesiones
2.Recibían una descripción de la manera de ser de Tom y tenían que evaluar la semejanza entre la descripción y las distintas profesiones (juicios de representatividad).
3. Recibían la misma descripción de Tom y además se les comunicaba que esta descripción se basaba en pruebas proyectivas.
Resultados:
• Los juicios de los del grupo 3 correlacionaban con los de semejanza del grupo 2.
• Correlación negativa entre estos y los del grupo 1.
Conclusiones: Los sujetos se basaban en la semejanza más que en la frecuencia. Realizaban juicios por representatividad de la descripción, ignorando la probabilidad a priori de que un individuo, del que conocen muy pocos datos, se dedique a una profesión determinada.
3) Insensibilidad a la capacidad predictiva del dato
Se manifiesta cuando se tiene en cuenta únicamente la evidencia que puede confirmar la hipótesis de que se parte y se ignora la evidencia que puede conducir a su falsación.
Se tienden a utilizar únicamente la información disponible que salta a la vista, sin tratar de inferir nada. Sin embargo, la información ausente también se tiene en cuenta en la formula de Bayes.
“Fiesta en el club Ruiz” El señor Pérez es miembro del club Ruiz, y está en una fiesta a la que solo han sido invitados profesores universitarios y hombres de negocios.
Se pide asignar la probabilidad de que el señor Pérez sea profesor universitario, para lo que se pueden realizar 4 preguntas:
1. ¿Qué porcentaje de los asistentes son profesores universitarios?
2. ¿Qué porcentaje de los miembros del club Ruiz están en la fiesta?
3. ¿Qué porcentaje de los profesores universitarios presentes en la fiesta son miembros del club?
4. ¿Qué porcentaje de los hombres de negocios presentes en la fiesta son miembros del club?
Las preguntas 1, 3 y 4 representan las P(H), P(D/H) y P(D/H ́); la 2 es irrelevante. Resultados:
• El 89,3% consideraron relevante la pregunta 3: asociación entre el dato disponible y la hipótesis.
• Sólo el 53,6% considero relevante la pregunta 4: asociación entre el dato y la hipótesis alternativa
4) Falacia de la conjunción
La probabilidad conjunta de 2 sucesos es siempre menor o igual que la probabilidad de cada suceso por separado sin embargo, los sujetos consideran más probable la ocurrencia simultánea de 2 sucesos, si ofrecen un modelo más representativo de la información inicial.
Ejemplo de Linda página 340 Se ofrece una descripción de Linda; sujetos tienen que asignar puntuaciones (1-8) a unas afirmaciones. 1: lo más probable; 8: lo menos probable. La mayoría de los sujetos consideraron más probable la afirmación h) “Linda es cajera en un banco y es feminista” que la afirmación f) “Linda es cajera en un banco”, a pesar de que h) es la conjunción de c) “linda es feminista” y f).
Este sesgo también se encuentra relacionado con la construcción de escenarios: las personas consideran más probable una situación que aparece como una conjunción de varios sucesos, formando un escenario más detallado y complejo, que otra situación más ambigua en a que únicamente se describe un suceso.
5) Regresión a la media
Las puntuaciones extremas en una medición, tienden a acercarse a la media en una medición posterior.
Sin embargo, se ignora la regresión a la media y se espera que las puntuaciones extremas se mantengan, basándose en la semejanza entre dos eventos relacionados. El monitor de vuelo observa que el aprendiz disminuye el rendimiento al ser felicitado, y cuando se le castiga por la mala ejecución, el rendimiento aumentaba.
Heurístico de accesibilidad
Asignar la probabilidad de un suceso o de un acontecimiento, en función de la facilidad con la que puede recordarse.
Puede conducir a resultados correctos, pues lo más frecuente es también lo más disponible, y su recuperación es más rápida. Sin embargo, lo más accesible no siempre es lo más probable.
Heurístico de accesibilidad: se utiliza en juicios en los que se pide la estimación de frecuencias; en tareas de recuerdo.
Variables que afectan:
Frecuencia.
Se recuerda mejor la información más reciente, impactante o nítida
Familiaridad. Es más fácil recordar los nombres conocidos o famosos
El impacto que haya causado un acontecimiento.
La información que está presente en una situación concreta es más accesible, adquiere mucha más relevancia y favorece que se ignoren otras alternativas que- no están presentes.
Efecto de la explicación: Se tiende a considerar mayor la probabilidad de un suceso que se ha explicado previamente, que la probabilidad del resto de las posibilidades. Investigaciones posteriores: no es necesario explicar, sino únicamente imaginar un resultado para aumentar su probabilidad percibida.
El heurístico de accesibilidad está estrechamente vinculado con el heurístico de simulación.
Heurístico de simulación: se utiliza en tareas de predicción; ya que se estimaría la probabilidad de un acontecimiento en función de la facilidad con que puede anticiparse o imaginarse. Considerar más probable una situación (un escenario), cuanto más fácil pueda construirse o imaginarse.
Los sesgos a que dan lugar estos factores y sus mecanismos de acción son parecidos a los producidos por la representatividad:
• Se ignoran las probabilidades a priori: cuando se dispone de información reciente impactante, aunque esta contradiga la información sobre la frecuencia real de un suceso conocido, esta se tendrá en cuenta sin pensar en su relevancia estadística. Accidente de aviación
1) SESGO EGOCÉNTRICO: pensar que las propias creencias son mayoritarias en la población; sesgo no se produce intencionadamente, sino que se presenta porque nuestras ideas son más accesibles. Se da en el plano social.
Se ignora la capacidad predictiva del dato: fijarse sólo en la información que está presente en una situación concreta, olvidándose del resto.
2) SESGO DE EXPLICACIÓN: estimar como más probable aquello que ha sido explicado previamente. Pedir a unos sujetos que expliquen por qué determinado candidato electoral debía resultar elegido, estos asignaron mayor probabilidad de éxito electoral a dicho candidato, tan sólo con haber imaginado el escenario de triunfo electoral
3) SESGO RETROSPECTIVO: probabilidad percibida de un suceso aumenta cdo los sujetos conocen el resultado final. Se preguntó a unos sujetos qué cosas, de una lista ofrecida, era probable que ocurriesen en el próximo viaje de Nixon a China y, posteriormente a haberse producido este, se les volvió a preguntar por las mismas. Los sujetos cambiaron sus estimaciones iniciales ajustándolas a lo que realmente había sucedido.
4) SESGO DE LA CORRELACIÓN ILUSORIA: dos sucesos altamente significativos o distintivos se asocian, dicha asociación queda establecida en la memoria y es más accesible y fácil de recordar, por lo que se estima mucho más frecuente de lo que en realidad es. Creación de estereotipos sociales.
Heurístico de anclaje y ajuste
Emisión de un juicio basado en algún valor inicial (obtenido mediante cualquier procedimiento, incluido el azar) que posteriormente se va ajustando, a medida que se añade más información, hasta producir la respuesta final.
La persona realizaría el juicio a partir de alguno de los rasgos del estímulo, y posteriormente, se ajustaría este primer juicio para que integre los rasgos restantes. Por tanto, la respuesta final estará sesgada hacia el valor inicial, tanto si es relevante para el problema como si no lo es.
Críticas de los heurísticos
Flexibilidad:
El mismo heurístico se utiliza en situaciones muy diferentes sin poder determinar cuáles son sus condiciones de aplicación; no se puede predecir cuál heurístico se aplicará en una situación concreta. Posiblemente se utilicen sucesivamente, considerando primero la información más accesible y seleccionando luego la más representativa.
Distintos heurísticos se utilizan para explicar la misma situación; algunos sesgos pueden ser debidos tanto a uno como a otro heurístico.
El mejor definido de los tres heurísticos es el de representatividad, seguido del de accesibilidad y por último el de anclaje.
Falta de validez externa:
Los resultados obtenidos en laboratorios no pueden extrapolarse a la vida cotidiana.
En el ambiente natural se producen situaciones más complejas que en el laboratorio.
Las personas no solo usan los datos que se les proporcionan ,también usan su conocimiento del mundo, correlaciones en su vida, percepciones sobre la intención oculta de las personas o la aplicación de reglas que conducen a conclusiones correctas.
Adquisición de la información: En situaciones de laboratorio, aparecen todas las hipótesis posibles y éstas son complementarias. Esta no es la situación habitual en la vida real, en la que rara vez se dispone de una lista exhaustiva de hipótesis ni de las complementarias (necesario para la aplicación de teorema de Bayes)
Precisión del juicio: En la vida diaria generalmente no existe un criterio objetivo con el que contrastar los juicios emitidos, lo que le va a evaluar la racionalidad de dichos juicios por consenso social, por relación entre el coste y el beneficio obtenido, o por su adecuación a la meta perseguida.
En algunos casos, los heurísticos resultarían estrategias más adecuadas que la norma estadística en el ambiente natural, ya que no siempre conducen a resultados erróneos. Por eso, cabe preguntarse por la adecuación del modelo bayesiano, como criterio con el que contrastar la precisión de los juicios humanos. Existen enfoques alternativos que tratan de explicar los resultados observados en tareas de juicios probabilísticas.
Enfoque de los modelos mentales
A) TEORÍA DE LOS MODELOS MENTALES DE JOHNSON-LAIRD Y BYRNE
Los sujetos no razonan de modo diferente cuando se enfrentan a problemas deductivos o inductivos: a partir de las premisas, construyen los modelos mentales que servirán de base a la conclusión. En la tarea de razonamiento deductivo, proponiendo que el juicio se resuelve con la construcción de un conjunto de modelos basados en la información de la que se dispone; la conclusión obtenida se considerará más o menos probable en función del número de modelos que apoyen o contradigan dicha conclusión.
Debido a las limitaciones de la memoria de trabajo, el sujeto no puede atender un no elevado de modelos, por lo que evalúa la frecuencia de los modelos a favor y en contra utilizando ilusiones cognitivas que sesgan el juicio. Cuando se razona sobre la probabilidad relativa de dos sucesos A y B con varios operadores, los sujetos pueden cometer errores al no representar de forma explícita los casos en los que no ocurren los sucesos.
Los estudios de razonamiento probabilístico se han centrado en los efectos producidos por el orden de presentación de la información y la congruencia o incongruencia de las fuentes.
Resultados: el orden de presentación de la información genera modelos mentales distintos y que la integración de la información representativa y la probabilística depende de la congruencia entre ambas. Ante una incongruencia entre las fuentes de información, el sujeto desatiende la información cuantitativa y basa sus juicios en la información representativa. Aunque los resultados siguen mostrando el valor de la representatividad en los juicios probabilísticos, se descarta la utilización de una estrategia de razonamiento heurística, puesto que se integran ambas fuentes de información (representativa y probabilística) cuando estas son congruentes. Incluso en el caso de fuentes incongruentes, tanto los tiempos empleados en la lectura de la segunda premisa como los tiempos de elección de la repuesta son mayores que en la condición de congruencia
La teoría de los modelos mentales rechaza el uso del heurístico de representatividad puesto que la información congruente se va integrando en la construcción de los modelos, ya sea esta información representativa o cuantitativa.
Se ha comprobado que los tiempos de solución son mayores cuando se presenta información incongruente aunque esta sea representativa; va en contra de la perspectiva de los heurísticos que defiende que la aplicación de los mismos sería una estrategia rápida.
Teoría de los modelos mentales reconoce que ante una incongruencia la información que prima es la representativa, pero aún en este caso se ralentiza la construcción de los modelos.
La facilidad para construir algunos modelos mentales o la rapidez con la que se pueden evocar, provocan que el sujeto se centre sólo en algunos de estos modelos sin tener en cuenta el resto; explicación próxima al heurístico de accesibilidad.
Explicación: el elemento central de la información condiciona la construcción de los modelos.
Explicación alternativa: las personas basan su respuesta en los modelos en los que se da una similitud entre las premisas y la conclusión.
B) TEORÍA DE LOS MODELOS MENTALES PROBABILÍSTICOS, GIGERENZER, HOFFRAGE Y KLEINBöLTING
Rechaza la asunción de irracionalidad de las personas; consideran que las teorías estadísticas no pueden entenderse como modelos normativos en los estudios sobre heurísticos, dado que los problemas tratan de un solo caso mientras que la probabilidad también se aplica sobre frecuencias o poblaciones.
Cuando el problema se presenta como frecuencias, en lugar de la probabilidad de un solo acontecimiento se encuentra que los sesgos de razonamiento decrecen.
Si la persona dispone de suficiente conocimiento para emitir un juicio, lo hará construyendo un modelo mental local que asociaría la estructura de la tarea con el conocimiento disponible. Si este conocimiento no es suficiente, es preciso construir un marco de inferencia, un modelo mental probabilístico, que consta de:
- una clase de referencia; sobre la que se plantea el problema
- una variable sobre la que se emite el juicio
- y una red de claves de probabilidad que generalmente covarían con la variable.
Razonamiento y Calibración
Calibración: grado de confianza que los sujetos asignan a sus propios juicios
Este juicio de segundo orden suele presentar un sesgo de sobreconfianza en los sujetos que se atribuyen una excesiva proporción de aciertos.
Tareas experimentales suministrar a los sujetos una serie de preguntas con dos alternativas y posteriormente pedirles que asignen un porcentaje de confianza a cada respuesta emitida.
Resultados: sujetos sólo aciertan en un 80% de los casos en los que aseguran estar totalmente seguros de las respuestas.
Explicaciones de este sesgo son:
- se genera más evidencia a favor de la hipótesis que en contra
- se atribuye fiabilidad absoluta a la memoria por falta de retroalimentación en la vida diaria (esto puede influir en tareas de reconocimiento)
- influyen factores motivacionales como la ilusión de control
el tipo de tarea: mejor calibración cuando se le pide asignar un rango de resultados que cuando se pide asignar confianza a un sólo evento
Críticas al tipo de tarea presentada: el hecho de que se compare el grado de confianza en un suceso único (que a respuesta sea correcta), con la frecuencia relativa de respuestas correctas.
Gingerenzer y col. desarrollan la teoría de los modelos mentales probabilísticos a partir de la construcción del marco de inferencia para explicar los resultados sobre calibración.
Si el sujeto no dispone del conocimiento suficiente construye un marco de inferencia: el modelo mental probabilístico; que consta de:
- Una clase de referencia
- Una variable
- Una red de claves de probabilidad
La teoría asume que los sujetos basan su respuesta en una de las claves de probabilidad que covarían con la variable, y que la confianza asignada a la respuesta iguala a la de la clave elegida.
Ello explicaría algunos errores de calibración cuando se pregunta con trampa sugiriendo una clave de mucha confianza; no explicaría otros fenómenos observados, como la asignación de altas probabilidades de acierto a tareas más difíciles y sin trampa.
La teoría de los modelos mentales no alude a la calibración para dar cuenta del sesgo de sobreconfianza.
La sobreconfianza se debería a la necesidad de satisfacción de los sujetos que seleccionarían los modelos mentales que conducen a conclusiones más creíbles o deseables.
Esta sobreconfianza será mayor cuanto más difícil sea la tarea y, por tanto, sean necesarios más modelos para llegar a una conclusión correcta.

